　本記事では、地上から撮影した写真を用いて航空機の飛行高度を推定する方法を説明します。以前の記事で、我が家上空に厚木基地の哨戒機P-3Cや輸送機C-130が低空飛行すると書きました。以前から、その飛行高度を知りたいと思っていたので、本記事で実際の写真を用いて計算したいと思います。

　飛翔体の大きさが分かっている場合、カメラの撮影パラメータや実際の大きさ、写真上の大きさを用いて、飛行高度を推定することができます。本稿では、対象物の形状や向きを考慮しない簡易な推定方法について説明しますが、対象物の向きを考慮すると、ここで示した方法よりもさらに低い高度となることにご注意ください。

1. 飛行高度推定の計算式
2. 高度推定のためのパラメータ
- 2.1 飛翔体の長さ
2.2 角度
2.3 視角の推定
- 2.3.1 カメラの焦点距離からカメラの画角を求める
- 2.3.2 カメラの画角と画像上の長さから視角を求める
3. 実際の写真から飛行高度を推定する
4. 最後に
付録A. 対象物の向きを考慮した推定について
付録B. iPhone5sの35mm判換算の焦点距離
付録C. 飛翔体の水平を仮定した場合の飛行高度推定
- C.1 高度推定式の導出
- C.2 推定結果
関連記事

1. 飛行高度推定の計算式

　飛翔体は棒状物体と仮定し、その長さを $L$ 、物体の中心は高度 $H$ にあり、飛翔体はカメラ視線と直交、天頂と視線が成す平面上にあると仮定します。ここで、 $\alpha$ を天頂方向とカメラを設置してある観測点 $O$ から対象物の視線が成す角度、 $d$ を点 $O$ から対象物中心までの距離、 $\theta$ を対象物の両端を観たときの視角とすると、飛翔物とカメラの位置関係は図1のようになります。

f:id:toranosuke_blog:20160912092026p:plain:w400

図1: 飛翔物とカメラの位置関係。

　この位置関係では対象物の高度 $H$ には、以下の関係があります。

$d=\frac{L}{2\tan(\theta/2)}$

$H=d\cos\alpha = \frac{L\cos\alpha}{2\tan(\theta/2)}$ .　　　　　(式1)

　従って、長さ $L$ 、角度 $\alpha$ 、視角 $\theta$ を知ることができれば、高度 $H$ を計算できます。

　ここでは、棒状物体は、天頂と視線が成す平面上にあると仮定していますが、棒状物体が視線を回転軸とした回転をした場合でも、視角 $\theta$ は変化しません。従って、この場合でも、上式を適用できます。

(追記: 2016/10/25) 上式では、視線方向と機体が直交することを仮定していますが、機体が水平に飛行することを仮定することもできます。 $\alpha$ が小さいときには、影響は小さいのですが、 $\alpha$ が大きくなると、影響を無視できません。このため、機体が水平であることを仮定した場合の飛行高度の推定を付録Cに追記しました。

2. 高度推定のためのパラメータ

　高度推定のためには、前節で説明した飛翔体の長さ $L$ 、角度 $\alpha$ 、視角 $\theta$ のパラメータを知る必要があります。以下では、それぞれのパラメータについて述べます。

2.1 飛翔体の長さ $L$

　飛翔体の長さ $L$ は、文献から知ることができます。今回、撮影した飛行機はC-130R輸送機で大きさは以下の通りです*1。

全長：29.8m
全幅：40.4m
全高：11.7m

　飛行機を見上げた画像からは、飛行機の高さはほとんど分からないので、以下では全高は用いません。

2.2 角度 $\alpha$

　角度 $\alpha$ は、計測器を用いて撮影したわけではないので精度よく知ることはできませんが、おおよその目分量で10°から30°程度です。角度 $\alpha$ は、(式1)の $\cos\alpha$ の項に影響を与えます。具体的には、 $\cos($ 30° $)$ = 0.86から $\cos($ 10° $)$ = 0.98の範囲となるので、最大1割強の差がでることになります。以下では、 $\cos\alpha$ の上限と下限の中央値をとって、 $\cos\alpha$ =0.92とし、誤差を±0.06として取り扱います。

2.3 視角 $\theta$ の推定

　視角 $\theta$ については、実際に撮影した画像から推定します。

2.3.1 カメラの焦点距離からカメラの画角を求める

　35mm判カメラの焦点距離と画角 $\Theta$ の関係は、以下の通り(参考：ウィキペディア「画角」)。

　 $\Theta = 2\tan^{-1}(\frac{36.0}{2FL})$ .

　撮影に用いたカメラはiPhone5sですが、iPhone5sカメラの35mm換算の焦点距離をFL=29.0mmとします(付録B参照)。このとき、水平方向の画角 $\Theta$ は、以下の通り、63.6°となります。

　 $\Theta = 2\tan^{-1}(\frac{36.0}{2\times29.0})=63.6$ °.

2.3.2 カメラの画角と画像上の長さから視角 $\theta$ を求める

　カメラの画角 $\Theta$ と画像上の飛翔体の長さ $k$ から、視角 $\theta$ を求める計算式について説明します。図2に示すように、カメラモデルはピンホールカメラでカメラ歪はなく、飛翔体は小さく、画像の中心付近で撮影されると仮定すると、以下の(式2)で視角 $\theta$ を十分な精度で近似計算できます。ここで、 $K$ は画像の水平方向の画素数でiPhone5sの場合3264画素、 $c$ は画像中心から飛翔体の中心までの画素数です。

　 $\tan(\theta+\beta) = \frac{b+k}{f}$
を変形すると、
　 $\frac{\tan\theta+\tan\beta}{1-\tan\theta\tan\beta} = \frac{b+k}{f} ~,$
$\tan\beta=\frac{b}{f}$ を代入し、
　 $\frac{\tan\theta+\frac{b}{f}}{1-(\tan\theta)\frac{b}{f}} = \frac{b+k}{f} ~,$
　 $f\tan\theta+b = \left(1-\frac{b\tan\theta}{f}\right)(b+k) ~,$
　 $f^{2}\tan\theta = kf - b (b+k)\tan\theta ~,$
　 $(f^{2}+b^{2}+bk)\tan\theta = kf ~,$
　 $\tan\theta = \frac{kf}{f^{2}+b^{2}+bk} ~,$
従って、
　　 $\theta = \tan ^{-1}\left(\frac{kf}{f^{2}+b^{2}+bk}\right) ~.$ 　　　　　　　　　　(式2)

ここで、
　 $f =\frac{K}{2\tan(\Theta/2)} ~,$
　 $b = c-\frac{k}{2} ~.$

f:id:toranosuke_blog:20161025130843p:plain:w350

図2：画像上の大きさ $k$ と視角 $\theta$ の関係。

3. 実際の写真から飛行高度を推定する

3.1 画像を用いた飛行高度の計算式

　これまでの計算式、及び、パラメータをまとめると、以下の通りです。

$H=d\cos\alpha = \frac{L\cos\alpha}{2\tan(\theta/2)}$ .　　　　　　　　　(式1)
C-130Rの長さ
- 全長：29.8m
- 全幅：40.4m
$\cos\alpha$ =0.92 $\pm$ 0.06
$\theta = \tan ^{-1}\left(\frac{kf}{f^{2}+b^{2}+bk}\right) ~.$ 　　　　　　　　　　(式2)
　ここで、
　　 $f =\frac{K}{2\tan(\Theta/2)} ~,$
　　 $b = c-\frac{k}{2} ~,$
　　 $K=3264 ~,$
　　 $\Theta = 63.6$ °

　従って、画像上のC-130Rの幅や長さ $k$ 、画像中心からの距離 $c$ を求めれば、高度 $H$ を計算することができます。

3.2 輸送機C-130Rの撮影画像

　iPhoneで撮影した3枚の画像を図3に示します。iPhoneでも、プロペラや尾翼などが意外と高い解像度で写ります。

f:id:toranosuke_blog:20161021200916j:plain:w400

f:id:toranosuke_blog:20160910112500j:plain

(a) 画像1

f:id:toranosuke_blog:20161021200937j:plain:w400

f:id:toranosuke_blog:20160910112511j:plain

(b) 画像2

f:id:toranosuke_blog:20161021201002j:plain:w400

f:id:toranosuke_blog:20160910114140j:plain

3.3 飛行高度の推定

　撮影した画像から画像上でのC-103Rの全幅や全長を求め、飛行高度を計算しました。

	画像1	画像2	画像3
画像中心からの距離 $c$ (ピクセル)	153	364	146
全長(ピクセル)	134	177	184
全長の視角(°)	2.92	3.78	4.00
全長から求めた高度(m)	537 $\pm$ 35	415 $\pm$ 27	392 $\pm$ 26
全幅(ピクセル)	187	205	203
全幅の視角(°)	4.07	4.38	4.41
全幅から求めた高度(m)	523 $\pm$ 34	486 $\pm$ 32	483 $\pm$ 31

　画像1から画像3は同じ機体を追いかけて撮影しているので、高度はほぼ同じと思いますが、推定値は400mから550m程度の値となりました。付録Aで説明していますが、機体が傾くと、推定される高度は、実際の高度よりも高い値となります。

　画像1は明らかに他の画像に比べても斜めからの撮影になっていますので、それに伴って、推定高度は高くなっています。いずれの写真でも、機体を斜めから撮影していますが、画像2と画像3の全長方向(機首から尾翼まで)が最も斜めの度合いが低いようです。実寸の機体の全長は29.8m、全幅は40.4mなので、全長と全幅の比は 1.35 となりますが、画像2と画像3の全長・全幅の比は、それぞれ 1.15 と 1.10 で本来の比よりも2割程度小さく、全長に比べて全幅がより短く映っていることからも判断できます。

　画像2と画像3の全長から推定した高度は、415mと392mでした。斜めに映っていることを考慮すると、それよりも若干低い高度で飛行していると思われます。

4. 最後に

　本記事では、写真から航空機の飛行高度を推定する方法を示しました。また、iPhoneで撮影したC-130R輸送機の画像から、我が家上空の飛行高度を推定したところ、400m程度の飛行高度であることが分かりました。

　この程度の高度で飛行することは頻繁にあるのですが、結構うるさいです。自衛隊さん、出来ればもう少し上空を飛行してもらえませんかね？

(2016/10/22)

付録A. 対象物の向きを考慮した推定について

　対象物の向きを考慮した場合の高度推定について説明します。

　図4に示すように機体が傾いた場合、本文で示した方法で計算される推定高度 $H$ は、本来の高度 $H'$ よりも大きくなります。これは、実際には低空を飛行しても、機体の傾きがあれば、傾きがないものとして高度を推定してしまうからです。

　もっと分かりやすく言うと、機体(棒状物体)が傾けば、小さく見えます。同じ大きさのものでも小さく見えれば、遠くにあると思ってしまうことと同じで、傾きが大きければ大きいほど、機体は小さく見えるために、推定高度はより高くなります。

f:id:toranosuke_blog:20160914235638p:plain:w300

図4: 機体が傾いた場合、推定高度 $H$ は本来の高度 $H'$ よりも高くなる。

　棒状物体モデルの場合、遠くて傾いていない機体と近くて傾いている機体の区別ができません。このため、棒状物体モデルの場合では機体に傾きがあると推定高度に誤差を生じさせます。しかし、航空機の形状を十字形でモデル化すると、傾きを考慮した飛行高度の推定式を導くことができ、より高い精度での推定が可能となります。具体的な計算方法を示そうかと思ったのですが、専門的で長くなるので、記事に含めませんでした。

付録B. iPhone5sの35mm判換算の焦点距離

　iPhone5sの35mm判換算の焦点距離は、AppleによるiPhone5sの技術仕様では公表されておらず、別の方法で調べる必要があります。以下では、公開されている情報からiPhone5sの焦点距離を推測します。

B.1 Exifデータでの35mm換算の焦点距離

　iPhone5sのカメラの35mm換算の焦点距離は、例えば、以下の記事では30mmと言われているようです。

　これらは、JPEG画像に含まれるExifの情報を根拠にしています。記事中のExifデータは「焦点距離4.1mm, 35mm判換算の焦点距離30mm」で、私の撮影した画像では、「焦点距離4.15mm, 35mm判換算の焦点距離29mm」と異なる数字となっています。カメラモジュールの変更、あるいは、ソフトウェア的な変更などなんらかの理由で、発表時のiPhone5sと現在のiPhone5s(購入はiPhone5sの発売当初)で違いがあることが分かります。

B.2 撮像センサの仕様から計算した35mm換算の焦点距離

　以下のブログに記載の方法に従って、iPhone5sのセンササイズ(4.89mm×3.67mm)から計算してみます。

ソニックムーブ, 「ARアプリとカメラの画角について」,2013/12/24.
- iPhone5sの撮像素子のスペック: "Image Sensor Relative Size Comparison Tool".

　カメラの焦点距離 $fl$ は、Exif情報の4.15mmと先のBrian Klugの記事にある値である4.12mm(他の記事でもよく記載される値)を用いて、35mm判換算の焦点距離 $f35$ を計算すると、次の値となります。ちなみに35mm判のサイズは36mm×24mmです。

水平幅を基準とした35mm判換算の焦点距離：
$f35$ ( $fl$ =4.15mm) = 36×4.15/4.89 = 30.55mm
$f35$ ( $fl$ =4.12mm) = 36×4.12/4.89 = 30.33mm
対角長を基準とした35mm判換算の焦点距離：
$f35$ ( $fl$ =4.15mm) = $\sqrt{36^2+24^2} \times 4.15/\sqrt{4.89^2+3.67^2}$ = 29.37mm
$f35$ ( $fl$ =4.12mm) = $\sqrt{36^2+24^2} \times 4.12/\sqrt{4.89^2+3.67^2}$ = 29.15mm

　ここで、水平幅と対角長の二つの基準があるのは、iPhone5sのカメラはアスペクト比4:3、35mm判カメラがアスペクト比3:2と一致せず、35mm換算の計算時に基準の取り方に選択肢があるためです。

　計算した値は、Exif情報の $fl$ =4.15mmを使うと、水平幅基準で30.55mm、あるいは、対角長基準で29.37mmとなります。対角基準の場合は、35mm換算焦点距離29mmのExifデータと矛盾しない値となります。

　ここで示した値の最小は29.15mm、最大は30.55mmで数％程度の違いです。今回の飛行機高度の推定には十分小さな差ですので、本稿ではExif情報の29mmをiPhone5sの焦点距離として取り扱います。

B.3 焦点距離は、水平基準か、対角基準か？

　Exifの規格*2では、アスペクト比が3:2でない場合の35mm換算の焦点距離の計算方法は規定されていないようです。このため、iPhone5sのExif情報の焦点距離29mmが、水平幅基準、あるいは、対角基準のいずれに基づいて計算されているのか分かりません。

　前記ソニックムーブのブログでは、iPhone5は水平基準で計算されていると推定されることから、本稿でもiPhone5sの場合も同様に水平基準から計算されているものと仮定します。

B.4 本稿で採用する焦点距離

　結論として、本稿では、iPhone5sの35mm判換算の焦点距離は、水平基準で計算された29mmとします。但し、推測誤差は5パーセント程度。

　5％程度の誤差であれば、自分で計測しても得られそうな精度ですね。

付録C. 飛翔体の水平を仮定した場合の飛行高度推定

C.1 高度推定式の導出

　図5の位置関係を仮定します。本文の仮定との違いは、飛翔体が水平であることと、天頂からの角度 $\alpha$ を飛翔体の中心ではなく、近い方の端に設けている点です。 $\theta$ が小さい場合には大きな影響はありません。また、もともとの $\alpha$ は目分量で決めているので、誤差が大きいので、無視できる範囲です(気になるのであれば、 $\theta$ 程度のバイアスを $\alpha$ に加えて補正すればよいでしょう)。

f:id:toranosuke_blog:20161025194045p:plain:w350

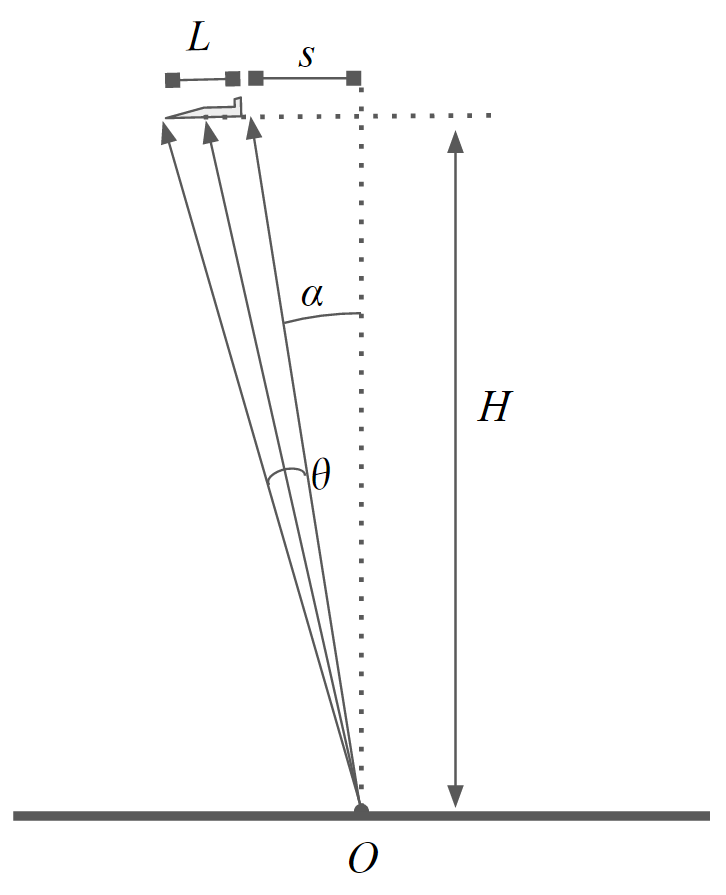
図5：飛翔体が水平航行することを仮定した場合の位置関係。

　このとき、次の関係式が得られます。

　 $\tan(\theta+\alpha) = \frac{L+s}{H}$
　 $\tan\alpha = \frac{s}{H}$

　第2式から得られる $s=H\tan\alpha$ を第1式に代入し、 $H$ を求めると、次式となります。

　 $H= \frac{L}{\tan(\theta+\alpha)-\tan\alpha}$

C.2 推定結果

　飛翔体が水平と仮定して計算した結果は、以下の通りです。全体的に30～40m程度、推定高度が低くなります。

	画像1	画像2	画像3
全長から求めた高度(m)(本文の方法)	537 $\pm$ 35	415 $\pm$ 27	392 $\pm$ 26
全長から求めた高度(m)(水平を仮定)	493 $\pm$ 68	379 $\pm$ 53	358 $\pm$ 51
全幅から求めた高度(m)(本文の方法)	523 $\pm$ 34	486 $\pm$ 32	483 $\pm$ 31
全幅から求めた高度(m)(水平を仮定)	475 $\pm$ 68	442 $\pm$ 63	439 $\pm$ 63

　この方法では、天頂方向と視線が方向がなす平面上に棒状物体がある必要がありますが、本文の方法では、その制限はありません。基本的に天頂から視線方向に棒状を見た場合には棒が小さく見えますので、そういう場合には、ここでの方法がより近い推定となり、一方、天頂方向と視線がなす平面に棒状物体が直交する場合には、水平飛行であっても大きさは変化しませんので、本文の方がより適切な推定方式となります。

　飛行機を十字形と考えると、真上に飛行機がある場合を除いて、本文の仮定(視線方向と全長・全幅の方向が直交する)と、ここでの仮定(水平飛行と物体の向きの仮定)が同時に成立することはありません(真上に来た時には２つの仮定が同時に成立し得る)。このため、本文の推定とここでの推定は、おおよその目安と思うことが必要です。

　より正確に推定するためには、機体の向きについての仮定を緩めて、推定式を導く必要があります。

*1:海上自衛隊, 「写真ギャラリー C-130R固定翼機」.

*2:「デジタルスチルカメラ用画像ファイルフォーマット規格 Exif 2.31」カメラ映像機器工業会規格 CIPA DC-008-2016.

時事随想

ニュースや新聞を見て、想ったことを綴った随想・論説集

写真からの航空機の飛行高度推定

1. 飛行高度推定の計算式